1.非线性误差的产生
由于涡街流量计传感器所测的并不是平均流速,而是漩涡发生体两侧的流速。对于湍流状态,不同的雷诺数下,流速分布规律是不同的,即不同的流速下具有不同的流速分布,进而说明了涡街流量传感器检测到的主要反映漩涡发生体两侧的流速,与管道平均流速的关系不是唯一确定的。这说明涡街流量传感器的非线性误差是其检测机理所决定的。在实际使用时,先绘出传感器的仪表常数与流体流速的试验曲线,据此得到不同流速段的实际仪表常数。本文应用MCS-51单片机系列的89C51将试验曲线事先固化于流量计的EPROM中,用户结合现场具体工作情况通过键盘输人平均仪表常数Kp的值(Kp=(Kmax+Kmin)/2),实现了涡街传感器的非线性修正。
2.仪表常数与流体流速的关系及分段补偿
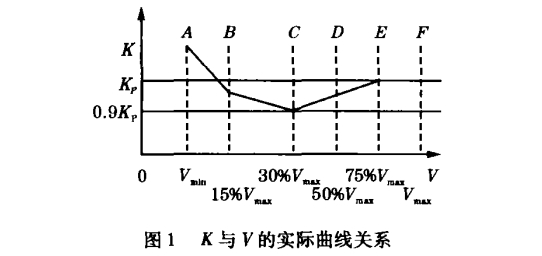
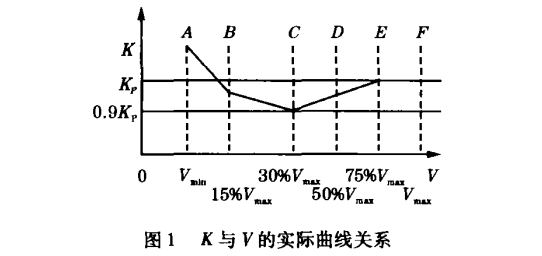
我们知道涡街流量计频率与流量成正比,理论上讲,涡街流量计输出频率与流速成正比,也就是说仪表常数恒定。实际上,由于流量计本身的因素导致两者之间存在一定程度的非线性误差。鉴此,我们做出了一条仪表常数与流速的实验关系曲线,如图1所示。图中各点坐标分别为A(Vmin,1.0049Kp),
B(15%Vmax,0.997Kp),C(30%Vmax0.992853Kp),D(50%Vmax,0.94883Kp),E(75%Vmax,Kp),F(Vmax,Kp)。
针对这种误差规律,我们采取分段补偿的方式进行误差修正。由图1可以看出,随着流速的降低,曲线偏离平均值越大,对此我们采用的方法可以达到两个目的:
(1)无论偏差值多大,只要它有规律可循,就可补偿修正,还可以把流量的下限即Vmin在坐标上向左移动,即扩大传感器的量程。
(2)根据精度要求合理划分区间,在误差大的低流速区间线段取密一些,在误差小的高流速区间可适当将区间放宽。
为了满足修正后非线性误差在0.3%以下的要求,我们根据理论分析和曲线规律,分别在12%Vmax、60%Vmax处增加两点(见图2),坐标分别为G(12%Vmax,Kp),H(60%Vmax,0.998Kp)。理由:①Vmin/Vmax=8%~9%;②DE曲线间无拐点且下凹;③AB曲线间无拐点且下凹。这样,把整个流速范围分成了六段,如表1。这样处理后,可修正非线性误差在0.3%以下。
3.补偿后非线性误差计算及验证
表2为补偿后各段仪表常数的非线性误差计算值。
下面用某厂生产口径为DN80的涡街流量计为例验证补偿效果。
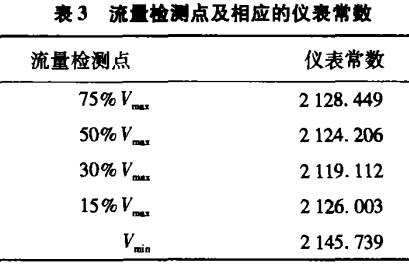
表3为原始检测数据。
平均仪表常数:
Kp=(Kmax+Kmin)/2=2132.4305
非线性误差:
δ=(Kmax-Kmin)/(Kmax+Kmin)x100%=0.62%
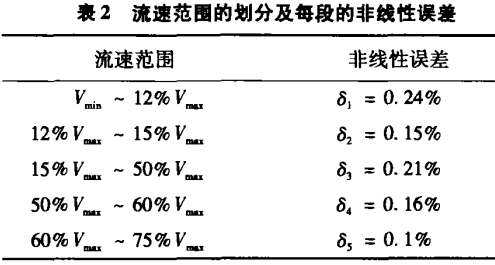
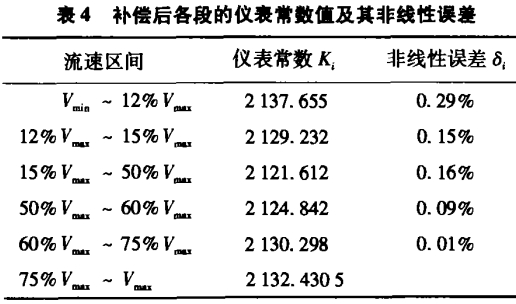
表4为补偿后的各段仪表常数以及非线性误差计算值。由此可见,补偿后精度得到了提高。
4.计算流量
瞬时流量计算公式:

Q=qvt
式中:fi、Ki-----第i频率段的漩涡分离频率和相应的仪表常数;t---累计时间。
 |


