1.声路角误差修正
??由于直接测量
超声波流量计角度较为困难,且其测量仪器精度不能达到要求,因此考虑在测量方式上进行优化,提出一种依据长度安装要求达到控制声路角的方法。

??图4所示为流量相对误差与声路角的关系。由图4可知,在声路角测量误差较小时,流量测量相对误差随声路角(安装角)大小的变化不明显,如图中红线(σθ=0.1%)所示。反之,若声路角测量误差较大,则流量相对误差随声路角的变化呈抛物线变化,如图中绿线(σθ=1°)所示,且存在一个最小值。声路角不变时,流量相对误差会随着绝对误差的增大而增大。
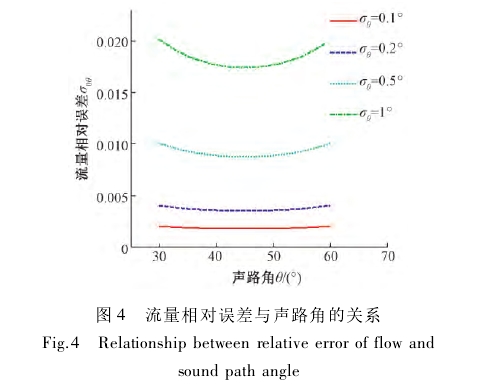
??令?σ/?θ=0,有θ=45°时,流量的相对误差σ0Q取最小。
2.K值的修正
??K系数与流体型态有关且随雷诺数变化而变化,研究不同型态下的K系数随雷诺数变化规律有利于流量补偿计算和提高测量精度。
??由式(24)可知,层流时的修正系数K=4/3,但对大管径来说,场内流态一般是紊流情况。因此,本文重点分析紊流时的
超声波流量计
系数K的修正。
??紊流时修正系数与雷诺数有关,经验公式为:
K=1.119-0.011xlgRe(25)
??依据式(25)可知.流量系数与雷诺数呈线性关系,雷诺数变化直接影响流量系数的取值。本文考虑根据雷诺数相关的变量来对K值进行修正。雷诺数计算公式为:

??式中:V为平均流速;D为管道内经;?为流体运动粘度。
??由式(26)可知,雷诺数大小与3个变量有关。当管径一定时,雷诺数会随着平均流速和流体粘度变化而变化。水的粘度随温度的变化而变化,温度变化会影响到雷诺数,进而影响流量修正系数K的值。因此找出粘度随温度的变化关系对K的准确性有着一定的影响。
??流体粘度受流体温度的影响具有非线性特点,通过拟合温度与运动粘度值,得到不同温度下水的运动粘度的曲线,如图5所示。
??多项式拟合表达式为:
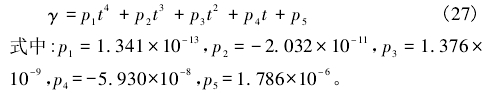
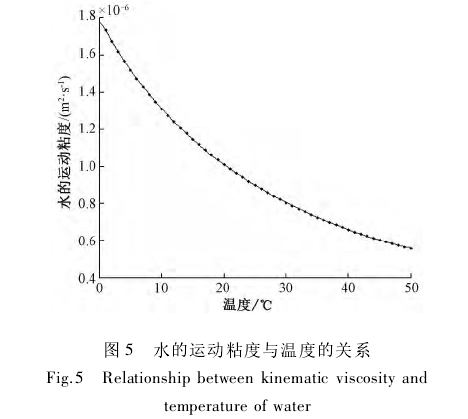
??随着温度的升高,水的粘度非线性特征愈发明显。在0~50℃范围内水的粘度值差值可达到1.2x10-6m2/s,对应的雷诺数误差为66.67%,不容忽视。
??将得到的拟合曲线依次代入式(19)、(20)得:
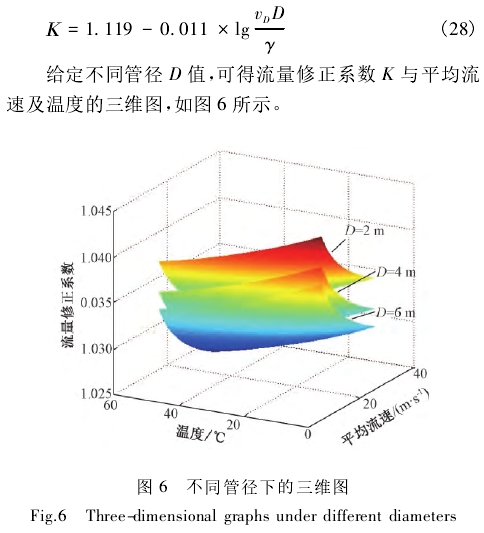
??由图6可以看出,同一管径条件下,
超声波流量计
系数随平均流速和温度的增加都呈非线性减小趋势。其他条件一定时,随着管径D的增大流量系数K值会减小。
??此修正方法将温度和流速变化与K值联系起来,两者任一值发生变化都能找到相对应的修正系数值,为准.确测得流量提供了一定的理论基础。
|


