1.流场仿真结果
??计算得到的
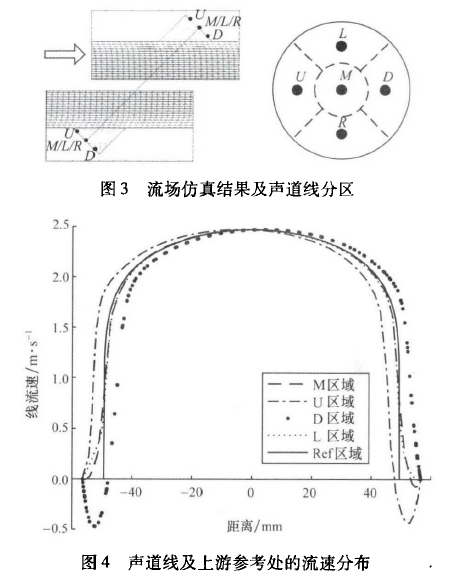
超声波流量计探头处流场如图3所示,探头附近存在旋涡。把探头端面分别分为5个区域,以5个区域的中点M、U、D、L、R作为计算依据,分别提取5条连线上的流速分布,比较不同区域的流速变化,如图4所示。各个点与中心M的距离为3.9mm。
??图4中横坐标表示声道方向探头面与声道中心的距离;纵坐标表示声道方向的流速,A至B方向流速为正;R区域与L区域流速分布相同;Ref是指参考位置即未受到探头扰流处,壁面连线之间的区域。探头A的D区域和探头B的U区域流场有明显的速度变化,这是因为在探头安装孔处形成了旋涡,流速在这两个区域内变化最为剧烈,而且相对流场而言,安装孔内的旋涡方向和大小并不相同;M区域和L区域处的流场相类似,受旋涡影响较小。
2.声场仿真结果
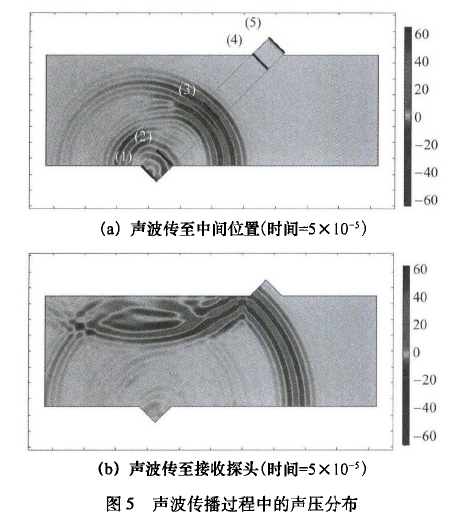
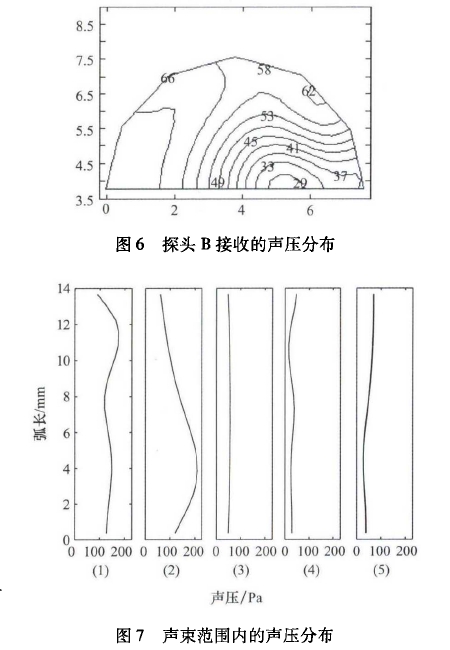
??图5展示了探头A发射超声波时,超声波的传播过程。在探头A、探头B的壁面处,超声波发生了反射,反射信号和原信号相互叠加,造成了接收面声压的不对称,进而影响传播时间的测量。探头B接收声压的分布情况如图6所示,声压在接收面上非均匀分布,在接收面上分布-一个低压区,低压区中心位于中心偏下游的位置。
??图7为超声传播过程中不同位置声压振幅的分布情况,其中位置1~位置5已在图5(a)中标注,统计的是声波经过该位置的声压变化的振幅。在探头A处的壁面反射造成了发射声压分布的畸变,在传输过程中逐渐减少了它的影响,所以探头B所接收的声压主要受到B处壁面反射的影响,在探头B附近低压中心从上游逐渐向下游移动。
3.传播时间及流速计算
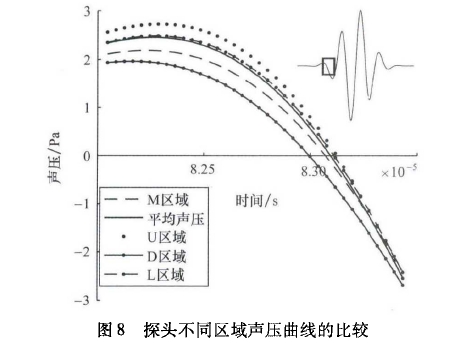
??由于旋涡和璧面反射的影响,靠近
超声波流量计
探头边缘区域的声压曲线存在一定畸变。探头B不同区域接收的声压与平均声压的关系如图8所示。其中实线代表平均声压,虚线代表M区域处的声压变化。声波传播过程中,受到不同声波传播路径和壁面反射的影响,接收面不同位置,接收声压幅值与过零点有明显的区别。M区域处声压曲线幅值略高于平均声压曲线、过零点与平均声压曲线接近;U区域和D区域处声压曲线过零点与平均曲线有较大差异。
??由于探头不同区域声压变化曲线的差异,采用平均声压曲线来计算时间差,平均声压的计算结果接近声压中心,而且有更好的稳定性。探头A、探头B接收到的平均声压变化曲线如图9所示,探头A由于流体的减速作用收到波形略晚,两个波形的相似度较高。利用互相关函数计算时差:
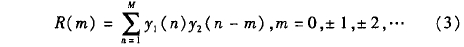
??式中,y1(m)和y2(m)为探头A、探头B接收声压信号;m为数据长度,由互相关理论,当互相关函数取得最大值的时间位移,对应的是两波形之间的时差。对R(m)进行优化求解,假设在m0点处取得最大值,可以求得时差△t:
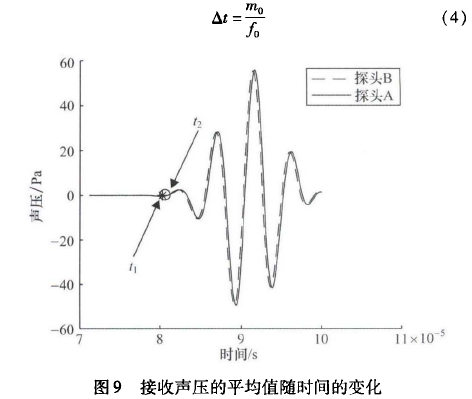
??实际流量计测量时,通常是通过正逆向传播时间T1、t2去和时差△t计算流速,由于流速远小于声速u0<
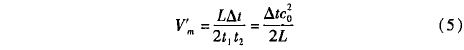
??式中,L为声道长度。将△t代人到式(5)中,可以解得声道方向的平均流速V'm。声场仿真计算中,△t=1.986x10-7s,L=113.0mm,求得V'm=I.928m/s。
??对比管道流场计算结果,对声束范围内流速取平均值,求得V'm=1.934m/s,未受到
超声波流量计
扰流区的声道方向平均流速Vm=2.247m/s,求得声场和流场计算的系统偏差E分别为一14.2%和-12.5%。两者的差异体现了壁面反射对修正系数的影响。
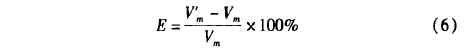
|


